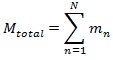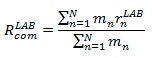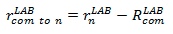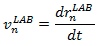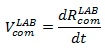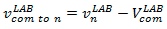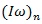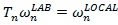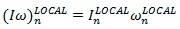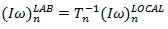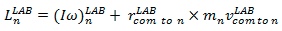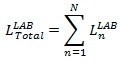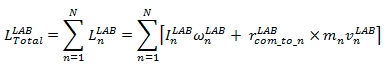Table of Contents
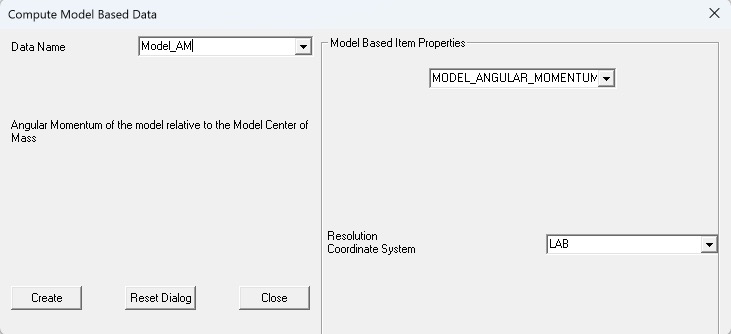
MODEL ANGULAR MOMENTUM
This page focuses on the the MODEL_ANGULAR_MOMENTUM model-based item in Visual3D. A full discussion on the theoretical underpinnings for Angular Momentum as a quantity can be found on Wikipedia.
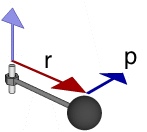
Angular Momentum of a Particle
Given a particle with momentum (p)
p = m v
The angular momentum (L) of this particle about a distal point is:
L= r x p
Model Center of Mass (COM)
The center of mass of an object is a theoretical point where all of the object’s mass can be considered to be concentrated. The Center of Mass of the model can be computed from the location of the center of mass of each segment.
Total Mass of the Model
Location of the center of mass of the model.
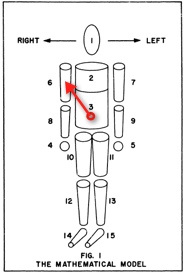
Segment COM relative to Model COM
The vector from the Model's COM to the COM of a segment is illustrated by the red vector in the figure below:
Velocity of the COM
Velocity of a Segment COM relative to the laboratory
Velocity of the Model COM relative to the laboratory
Velocity of a vector from the Segment COM to the Model COM in Laboratory coordinates.
Segment Angular Moment in Local Coordinates
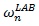 = Segment angular velocity in Lab Coordinates
= Segment angular velocity in Lab Coordinates
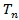 = Segment orientation matrix, which transforms a vector from Lab coordinates to Local coordinates
= Segment orientation matrix, which transforms a vector from Lab coordinates to Local coordinates
Compute the segment angular velocity in Segment Local Coordinates
Segment Angular Moment in Lab Coordinates
Angular Momentum of one Segment Relative to the COM
The angular momentum for one segment about the total body center of mass in Laboratory Coordinates is:
Angular Momentum of Model Relative to the COM
Now that all the angular moment values in a common coordinate system, we can simply add them.
The angular momentum for the total body about the total body center of mass is:
Where N = total number of segments
Note: The tricky calculation is 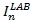 so the algorithm works around this issue by not actually calculating the value.
so the algorithm works around this issue by not actually calculating the value.
References
Much of the contents of this page are courtesy of Fred Yeadon.
- Yeadon, M.R. 1993. The biomechanics of twisting somersaults. Part I: Rigid body motions. Journal of Sports Sciences 11, 187-198.
- Yeadon, M.R. 1993. The biomechanics of twisting somersaults. Part II: Contact twist. Journal of Sports Sciences 11, 199-208.
- Yeadon, M.R. 1993. The biomechanics of twisting somersaults. Part III: Aerial twist. Journal of Sports Sciences 11, 209-218.
- Yeadon, M.R. 1993. The biomechanics of twisting somersaults. Part IV: Partitioning performance using the tilt angle. Journal of Sports Sciences 11, 219-225.
- Yeadon, M.R. 1993. Twisting techniques used by competitive divers. Journal of Sports Sciences 11, 4, 337-342.