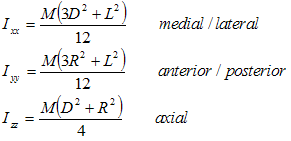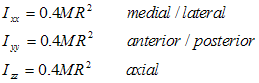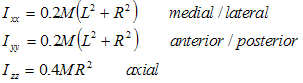Table of Contents
Segment Inertia
Visual3D computes the moment of inertia of a segment from the segment's mass, proximal and distal radii, and geometry. The default Visual3D segments are treated as geometric objects that have inertial properties based on their shape in accordance with Hanavan's mathematical model of the human body.
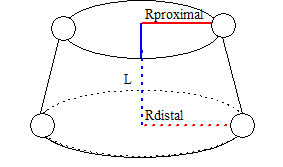
Inertial properties of a Cone (Conical Frustrum)
Visual3D's Cone segment geometry is, to be precise, a conical frustrum. A frustra of right cones is created by cutting the top off of a cone such that the cut is parallel to the base of the cone.
For a unit length, the center of mass relative to the proximal end of the segment is located at:
A Cone segment with mass M and length L has the following inertial properties:
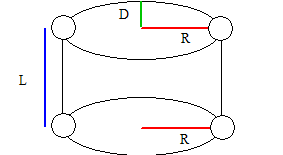
Inertial properties of an Elliptical Cylinder
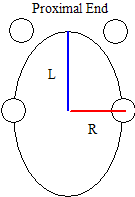
Visual3D's Cylinder segment geometry is a right elliptical cylinder, which is a cylinder with elliptical cross-sections.
The distance from the proximal end of the segment to the center of mass of the segment is
CG_from_proximal_end = 0.5*L
In Visual3D's default coordinate system, the moment of inertia of a cylinder is therefore:
Note that Visual3D uses the radius at the distal end of the segment as the radius of the cylinder.
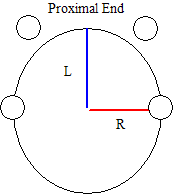
Inertial Properties of a Sphere
For segments modelled as a Sphere, Visual3D requires a proximal segment radius and a distal segment radius. The inertial properties of the segment are calculated using only the distal radius, however, the proximal radius is still required to determine the location of the proximal segment end.
If both a medial and a lateral target are used at one end of a segment during subject calibration, then the radius at that end is determined to be one-half of the distance between these targets. If only a single target is used at the end of a segment then a qualifier, either DIST_RAD or PROX_RAD, must be used.
One notable difference arises in creating spherical segments. Visual3D expects the distal targets to be located at 50% of the distance between segment ends. This allows the distal radius to produce a realistic measure of the dimension of the sphere.
The distance from the proximal end of the segment to the center of mass of the spherical segment is
CG_from_proximal_end = L
Within Visual3D's default coordinate system, then, the moment of inertia of a sphere is:
Note that Visual3D uses the radius at the distal end of the segment as the radius of the sphere. The length of the sphere is determined from the distance between the segment's proximal and distal ends.
Inertial Properties of an Ellipsoid
Visual3D also allows segments to be defined as an Ellipsoid, or deformed sphere.
The distance from the proximal end of the segment to the center of mass of an ellipsoid segment is given by:
CG_from_proximal_end = L
Within Visual3D's default coordinate system, the moment of inertia of an ellipsoid is:
Visual3D uses the radius at the distal end of the segment as the radius of the ellipsoid. The length of the ellipsoid is calculated as tghe distance between the sgement's proximal and distal ends.
Alternative Approaches
The user is free to modify segment characteristics away from Visual3D's defaults for both inertial parameters and coordinate systems.
Adjusted Zatsiorsky-Seluyanov's segment inertia parameters
It is possible to use the Adjusted Zatsiorsky-Seluyanov's segment inertia parameters in Visual3D instead of the default parameters from Dempster and Hanavan.
These inertial parameters adjust the original Zatsiorsky-Seluyanov segment inertia parameters from using bony landmarks as reference points to using joints centres instead since these more commonly used in biomechanics.
Entering Inertial Values Using Expressions
Visual3D allows the user to put expressions into the edit boxes, which means that any mathematical expression or regression equation can be used to express a segment's inertial properties and center of mass.
See the page covering entering inertial values using expressions for more details.
Coordinate System Transformations
Visual3D allows users to flexibly express a segment's moment of inertia in any coordinate system. See the page on transforming segment moments of inertia for complete details.
References
- Hanavan E. (1964) A Mathematical Model for the Human Body. Technical Report, Wright-Patterson Air Force Base