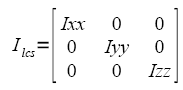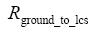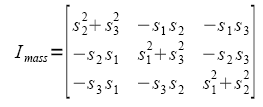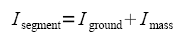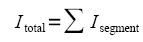Transforming moment of inertia from one Coordinate System into Another Coordinate System

Let the Inertia Tensor of Segment (foot or shank) in it’s own local coordinate system (f) be given:

Note: These are the values stored in Visual3D and viewable in the segment properties.

Find the value of this inertia tensor in any other reference frame (for example, ground) using the following equation:

Where 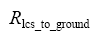is the rotation matrix that transforms a vector from it's own coordinate system (lcs) to the ground coordinate system

and is its transpose.

The above expression does not include the terms due to the parallel axis theorem (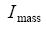) which are:

where the vector s defines the location of hte segment's center of mass relative to ground.

The total Inerties 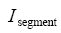for the segment is:

To find the total moment of inertia of all segments relative to ground you add the individual segment inertias:

This entire procedure is outlined nicely by Fred Yeadon in the following series of articles.

Yeadon, M.R. (1993). The biomechanics of twisting somersaults. Part I: Rigid body motions. Journal of Sports Sciences 11, 187-198.

Yeadon, M.R. (1993). The biomechanics of twisting somersaults. Part II: Contact twist. Journal of Sports Sciences 11, 199-208.

Yeadon, M.R. (1993). The biomechanics of twisting somersaults. Part III: Aerial twist. Journal of Sports Sciences 11, 209-218.

Yeadon, M.R. (1993). The biomechanics of twisting somersaults. Part IV: Partitioning performance using the tilt angle. Journal of Sports Sciences 11, 219-225.