HAS-Motion Software Documentation

This page contains a list of all of Evaluate_Expression's functions that are used to find a line or plane of best fit to your data.

Best_Fit_Plane(signal, start_event_signal, end_event_signal) - Finds a plane that fits the path of a point from a start event to an end event. The resulting plane is defined by 4 components.

The general form of the equation of a plane in 3D is ax+by+cz+d = 0 where 𝑎, 𝑏, and 𝑐 are the components of the normal vector which is perpendicular to the plane or any vector parallel to the plane.

If (𝑥0,𝑦0,𝑧0)is a point that lies on the plane, then 𝑑=−(𝑎𝑥0+𝑏𝑦0+𝑐𝑧0) and as 𝑎𝑥+𝑏𝑦+𝑐𝑧−(𝑎𝑥0+𝑏𝑦0+𝑐𝑧0)=0.

The result of the Best_Fit_Plane function is a signal with the fource components (a,b,c,d)

! Example: Compute a Best_Plane_Fit for one signal across a range of frames
Evaluate_Expression
/EXPRESSION=Best_Fit_Plane(CURRENT_SIGNAL,EVENT_LABEL::ORIGINAL::START,EVENT_LABEL::ORIGINAL::END)
/SIGNAL_TYPES=TARGET
/SIGNAL_FOLDER=ORIGINAL
/SIGNAL_NAMES=LSK_1
/RESULT_TYPES=METRIC
/RESULT_FOLDERS=PROCESSED
/RESULT_NAME=LSK1_PLANE
/APPLY_AS_SUFFIX_TO_SIGNAL_NAME=TRUE
;

! Example: Compute a Best_Plane_Fit for multiple signals at each frame of data
Evaluate_Expression
/EXPRESSION=Best_Fit_Plane(CURRENT_SIGNAL)
/SIGNAL_TYPES=TARGET
/SIGNAL_FOLDER=ORIGINAL
/SIGNAL_NAMES=LSK_1+LSK_2+LSK_3
/RESULT_TYPES=DERIVED
/RESULT_FOLDERS=PROCESSED
/RESULT_NAME=LSK_PLANE
/APPLY_AS_SUFFIX_TO_SIGNAL_NAME=TRUE
;

Best_Fit_Circle(signal, start_event_signal, end_event_signal) - Fits a 2D circle to the path of a signal.

The algorithm computes a best fit plane to the data, rotates this plane into a principal plane, computes the center and radius, the rotates these values back into the original plane. The result is 4 components:

1. the origin's X-coordinate;
2. the origin's Y-coordinate;
3. the origin's Z-coordinate; and
4. the radius.

Best_Fit_Sphere(signal,start_event_signal,end_event_signal) - Fits a 3D sphere to the path of a signal.

! Example : Fit a sphere to 6 points on a DIAMOND

! Create 6 TARGETS representing the Vertices
Create_Target
/SIGNAL_NAMES=V1
! /SIGNAL_DESCRIPTION=
/EXPRESSION=VECTOR((0.5+0*FRAME_NUMBERS::ORIGINAL::FRAMES),0,0)
! /INCLUDE_CALFILE=FALSE
;

Create_Target
/SIGNAL_NAMES=V2
! /SIGNAL_DESCRIPTION=
/EXPRESSION=VECTOR((-0.5+0*FRAME_NUMBERS::ORIGINAL::FRAMES),0,0)
! /INCLUDE_CALFILE=FALSE
;

Create_Target
/SIGNAL_NAMES=V3
! /SIGNAL_DESCRIPTION=
/EXPRESSION=VECTOR((0,0.5+0*FRAME_NUMBERS::ORIGINAL::FRAMES),0)
! /INCLUDE_CALFILE=FALSE
;

Create_Target
/SIGNAL_NAMES=V4
! /SIGNAL_DESCRIPTION=
/EXPRESSION=VECTOR((0,-0.5+0*FRAME_NUMBERS::ORIGINAL::FRAMES),0)
! /INCLUDE_CALFILE=FALSE
;

Create_Target
/SIGNAL_NAMES=V5
! /SIGNAL_DESCRIPTION=
/EXPRESSION=VECTOR((0,0,0.5+0*FRAME_NUMBERS::ORIGINAL::FRAMES))
! /INCLUDE_CALFILE=FALSE
;

Create_Target
/SIGNAL_NAMES=V6
! /SIGNAL_DESCRIPTION=
/EXPRESSION=VECTOR((0,0,-0.5+0*FRAME_NUMBERS::ORIGINAL::FRAMES))
! /INCLUDE_CALFILE=FALSE
;

Evaluate_Expression
/EXPRESSION=Best_Fit_Sphere(CURRENT_SIGNAL)
/SIGNAL_TYPES=TARGET
/SIGNAL_FOLDER=ORIGINAL
/SIGNAL_NAMES=V1+V2+V3+V4+V5+V6
/RESULT_TYPES=DERIVED
! /RESULT_FOLDERS=PROCESSED
/RESULT_NAME=SPHERE
! /APPLY_AS_SUFFIX_TO_SIGNAL_NAME=FALSE
;

Note that TARGETS are created and the sphere computed has each TARGET on its surface.

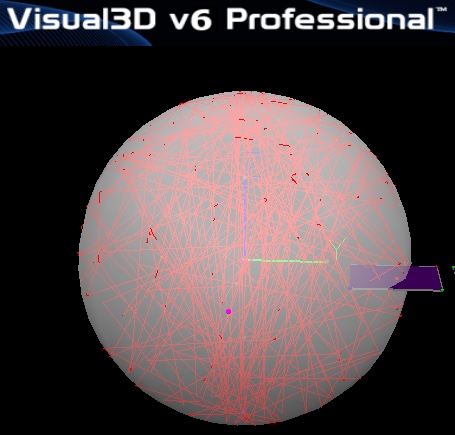
! Example : Create a TARGET where each frame is on a random location on the surface of a sphere of radius 1
Evaluate_Expression
/EXPRESSION=RAND(-PI(),PI(),FRAME_NUMBERS::ORIGINAL::FRAMES)
/RESULT_TYPES=DERIVED
/RESULT_FOLDERS=RADIUS
/RESULT_NAME=VERTICAL
! /APPLY_AS_SUFFIX_TO_SIGNAL_NAME=FALSE
;

Evaluate_Expression
/EXPRESSION=RAND(0,2*PI(),FRAME_NUMBERS::ORIGINAL::FRAMES)
/RESULT_TYPES=DERIVED
/RESULT_FOLDERS=RADIUS
/RESULT_NAME=HORIZONTAL
! /APPLY_AS_SUFFIX_TO_SIGNAL_NAME=FALSE
;

Create_Target
/SIGNAL_NAMES=SPHERE
! /SIGNAL_DESCRIPTION=
/EXPRESSION=VECTOR(
COS(DERIVED::RADIUS::VERTICAL)*COS(DERIVED::RADIUS::HORIZONTAL),
-COS(DERIVED::RADIUS::VERTICAL)*SIN(DERIVED::RADIUS::HORIZONTAL),
SIN(DERIVED::RADIUS::VERTICAL))
! /INCLUDE_CALFILE=FALSE
;

Evaluate_Expression
/EXPRESSION=Best_Fit_Sphere(CURRENT_SIGNAL)
/SIGNAL_TYPES=TARGET
/SIGNAL_FOLDER=ORIGINAL
/SIGNAL_NAMES=SPHERE
/RESULT_TYPES=DERIVED
! /RESULT_FOLDERS=PROCESSED
/RESULT_NAME=SPHERE
! /APPLY_AS_SUFFIX_TO_SIGNAL_NAME=FALSE
;

Simple_Linear_Regression(signal1, signal2, start_event, end_event); - Fits a signal to a line given by the equation Y = mX + b where

Signal = m Signal1 + b

An explanation of the calculation can be found here or here.

Signal1 and Signal2 are both one-component signals and the resulting METRIC contains 6 components:

1. Slope = m → Component 1
2. Intercept = b → Component 2
3. Siga = uncertainty in m → Component 3
4. Sigb = uncertainty in b → Component 4
5. Chi2 = chi square → Component 5
6. Q = The R^2 statistic → Component 6