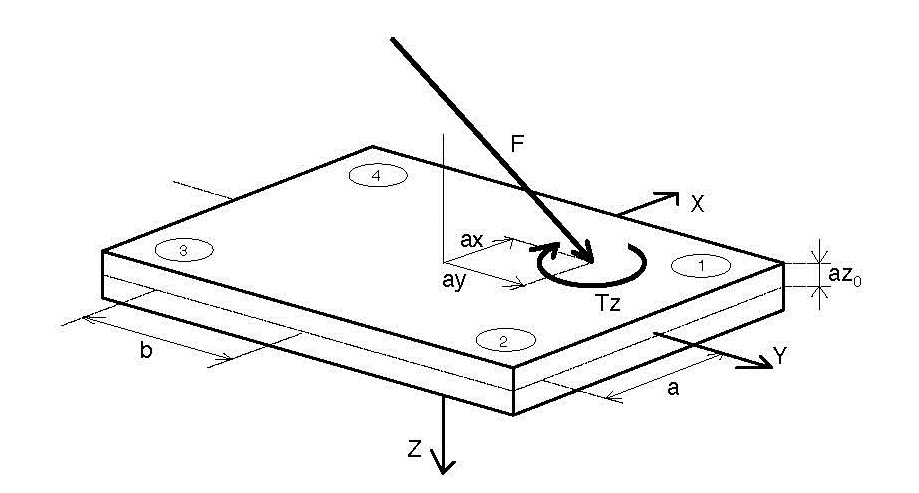
A Type 3 force platform records information according to its four corners, which are named 1, 2, 3, and 4.

A Type 3 force platform records 8 ANALOG channels containing the following information:

[Original Analog] = [Fx12, Fx34, Fy14, Fy23, Fz1, Fz2, Fz3, Fz4]

Note that a Type 7 force platform has the same analog channels as a Type 3 force platform but also includes a CalMatrix. Alternatively, a Type 3 force platform can be thought of as a Type 7 force platform where the CalMatrix is the identity matrix.

Calculating the desired force signals in the force platform's coordinate system consists of the following steps:

1. Compute baselines by averaging the analog signals for the specified FP_ZERO frames
2. Subtract each channel's baseline from its recorded signal
3. Calculate the Groud Reaction Force
4. Apply a threshold
5. Transform the signals into the Laboratory Coordinate System

The Force vector for a Type 3 force platform is calculated as follows:

Force[X] = Fx12+Fx34
Force[Y] = Fy14+Fy23
Force[Z] = Fz1+Fz2+Fz3+Fz4

The COFP signal for a Type 3 force platform is calculated as follows:

COP[X] = (-M[Y]/Force[Z]) + a
COP[Y] = ( M[X]/Force[Z]) + b
COP[Z] = az0

Where

a = Origin.X
b = Origin.Y
az0 = Origin.Z

M[X] = b*( Fz1 + Fz2 - Fz3 - Fz4) + az0*(Fy14 + Fy23)
M[Y] = a*(-Fz1 + Fz2 + Fz3 - Fz4) - az0*(Fx12 + Fx34)
M[Z] = b*(-Fx12 + Fx34) + a*(Fy14 - Fy23)

The FreeMoment signal for a Type 3 force platform is calculated as follows:

FreeMoment[X] = 0
FreeMoment[Y] = 0
FreeMoment[Z] = M[Z] + Force[Y]*(M[Y]-az0*Force[X]) + Force[X]*(M[X]+az0*Force[Y])

The transformation is defined by the location of the force platform corners, and is common to all force platforms.