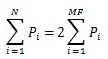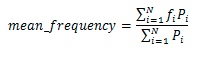The power in a signal can be computed from the DFT coefficients.

The form of the DFT is as follows:

p(t)= p0 + p1 sin(w t) + p2 cos(w t) + p3 sin(2w t) + p4 cos(2 w t) + ….

where w = 2 * PI * Base_Frequency

the power at a given frequency is given as the sum of the squares of the coefficients.

For example, the power at the Base_Frequency is given by (p1^2 + p2^2) the power at 2 * Base_Frequency is given by (p3^2 + p3^2)

Metric_Compute_Power_From_DFT_Coefficients /SIGNAL_TYPES= ! /SIGNAL_NAMES= ! /SIGNAL_FOLDER=DFT ! /RESULT_SUFFIX=_POWER ! /RESULT_FOLDER=DFT ; Additional (starting in Visual3D Version 5) the Mean and Median Frequency are computed.

These two metrics are commonly used to describe changes related to muscle fatigue.

The resulting Metric signal has two components.

The first component is the frequency. The second component is the power at the associated frequency.

The Median Frequency is the Frequency at which the Integral of the Power Spectrum to that Frequency equals half the Integral of the Total Power Spectrum (e.g. divides the power spectrum in two)

where MF = Median Frequency

The Mean Frequency is the Ratio of the Integral of the Frequency*Power over the Integral of the Power.

An additional result signal appended with _STATS is also created.

This signal contains the median frequency (component 1) and mean frequency (component 2)